Chaos may enhance expressivity in cerebellar granular layer

著者： Keita Tokuda, Naoya Fujiwara, Akihito Sudo, Yuichi Katori
掲載誌： Neural Networks, Vol. 136, pp. 72–86 (2021)
受賞： 2022年度 日本神経回路学会 論文賞

本研究は、小脳の顆粒細胞層において、情報表現の豊かさにカオス的なダイナミクスが関与している可能性を提案したものです。 顆粒細胞層は、小脳前核（たとえば橋核）からの苔状線維入力が集まる領域であり、小脳の入力層に相当します。 ヒトではおよそ千億にも及ぶ顆粒細胞が存在し、脳全体の神経細胞の大部分を占めると言われています。 そのため、この領域でどのような計算や情報処理が行われているのかは、長年にわたって大きな関心を集めてきました。

小脳は、古くから素早く正確な運動制御に重要な役割を果たすことが知られています。 特に、小脳依存的学習である瞬目反射学習に関する多くの研究により、 「特定の感覚刺激に対して、特定の運動出力を精密なタイミングで生成する」 という時間精度の高い処理を小脳が担っていることが明らかにされています1)。

さらに顆粒細胞は、このようなタスクにおいて、 「特定の入力後に、一定の遅れをもって特定の活動パターンを示す」 という役割を持つことが示唆されています。 たとえば、ある刺激（音など）が与えられてから数百ミリ秒後に、特定の顆粒細胞群が活動するというように、 顆粒細胞層の活動が入力からの経過時間を符号化していると考えられます。

興奮性の顆粒細胞と抑制性のゴルジ細胞は相互に結合し、リカレント構造を形成しています。 このリカレント回路における非線形ダイナミクスが、時間依存的な活動を生み出すという理論モデルがこれまでに提案されています2)。 また、山﨑・田中らは、この考えをさらに発展させ、 小脳回路をレザバー計算を行う「リキッドステートマシン」として捉えることを提案しました3)。

本研究の着想は、Vervaekeらの報告4)に端を発しています。 彼らは、小脳顆粒細胞層の抑制性細胞であるゴルジ細胞が、ギャップジャンクションを介して密に結合していること、 そしてこの結合がむしろ細胞間の「脱同期化」を引き起こすことを示しました。 ギャップジャンクションは隣接細胞間の細胞質をつなぐ構造であり、電気的結合（電気シナプス）として知られています。 一般的には電気的結合は同期化をもたらすと考えられますが、Vervaekeらの研究ではその逆の現象が観察されました。

この結果は、藤井宏・津田一郎らの研究5)で示された、 ギャップジャンクション結合系におけるカオス的な神経活動の報告と非常によく似ていました。 津田らは、拡散的結合を介して神経ネットワークにカオス的なダイナミクスが生じうることを理論的に示していました。

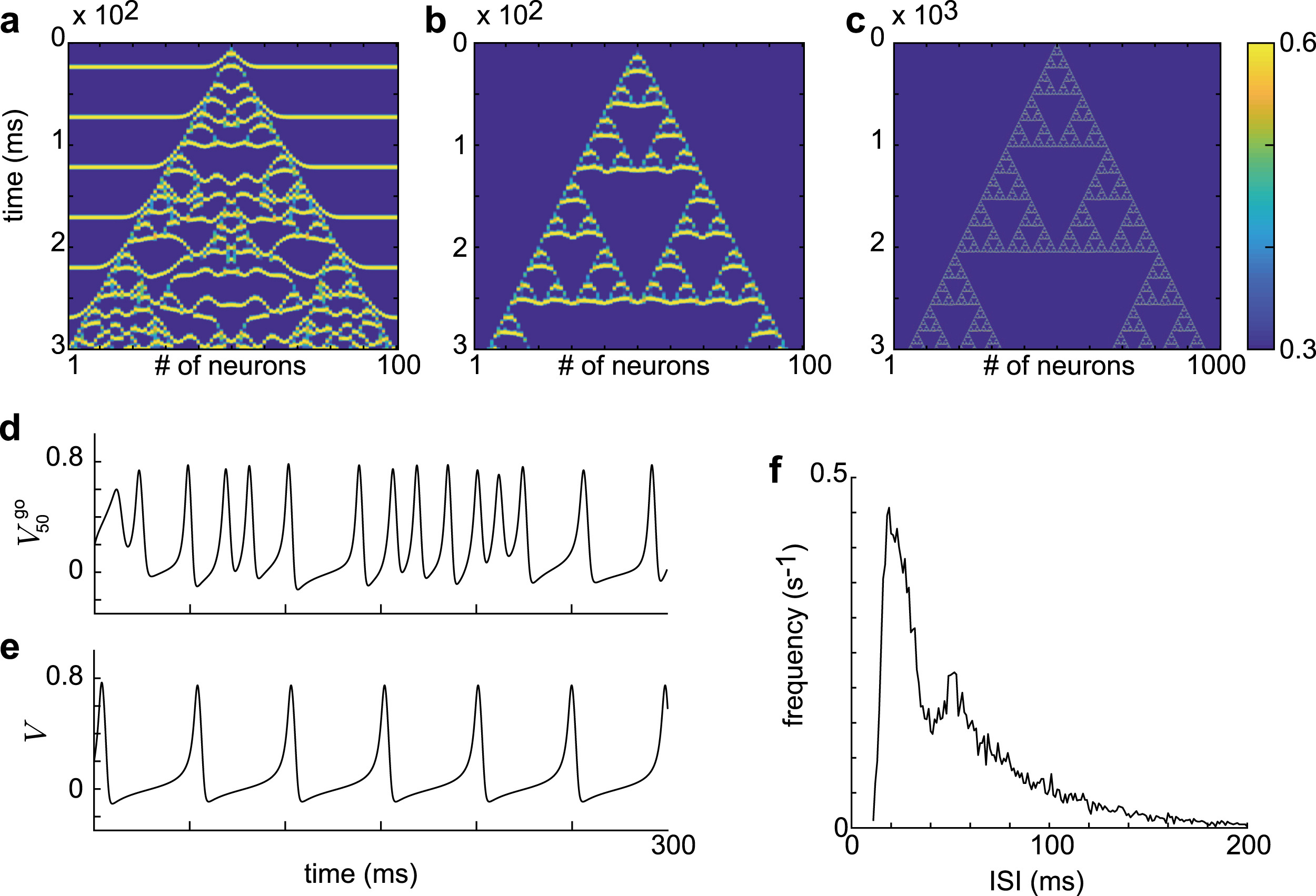
ギャップジャンクションによって生じる単純な小脳型リザーバーモデルのカオス的ダイナミクス
図2　Tokuda らによる論文 (Neural Networks, 136, 72–86, 2021) から転載。 © Tokuda et al. 2021. 本図は CC BY 4.0 ライセンスのもとで公開されています。 ギャップジャンクションによって誘発されるカオス的ダイナミクスは、一次元の連鎖構造をもつ単純なリザーバーモデルで再現される（式(1)〜(3)、図1(a)）。 (a) わずかな正の定常入力を与えたときのモデルのダイナミクス。カラーマップは膜電位の時間変化を示す。 (b–c) 弱い定常的な抑制入力のもとでシェルピンスキー・ギャスケット状のパターンが現れる。 (b) ではニューロン数 N = 100、(c) では Ngo = 1000。 (d) (a) における50番目のニューロンの膜電位の時間変化。 (e) 小さな正の定常入力下で孤立した μ モデルニューロンが示す周期的活動。 (f) カオス的ダイナミクスにおけるニューロンの発火間隔（ISI）の広い分布。(a) の50番目のニューロンのデータを 1 × 103 秒間示している。ビン幅は1 ms。

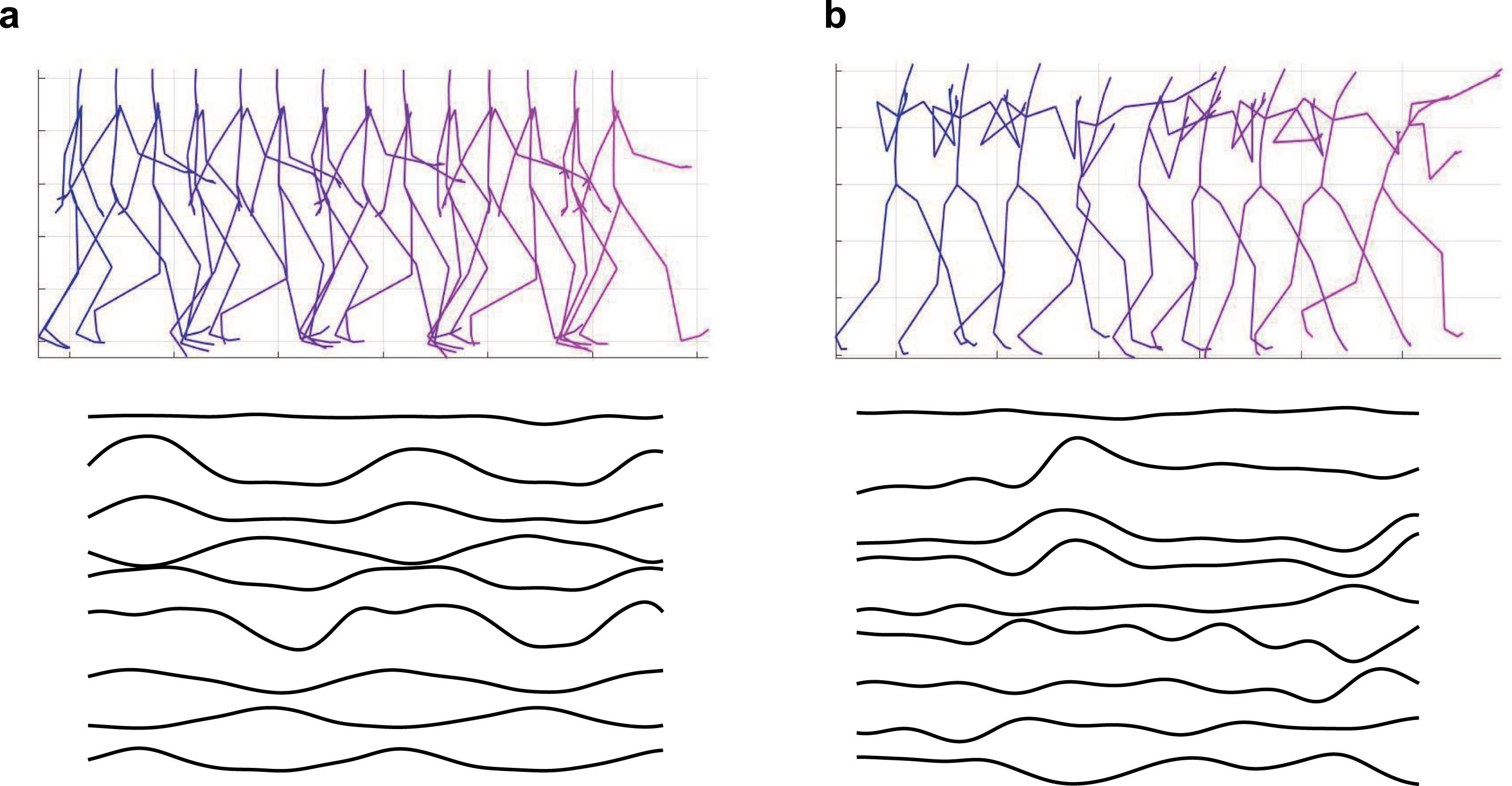
そこで本研究では、ゴルジ細胞間のギャップジャンクションがカオス的ダイナミクスを生み出すとき、 それが小脳顆粒細胞層の情報表現にどのような効果をもたらすかを理論的に検討しました。 カオス的な結合をもつモデルを構築し、レザバー計算の枠組みで評価した結果、 系のカオス性の指標（リアプノフ指数やリアプノフ次元）と、 出力の多様性（RMSE）との間に強い相関が確認されました。 この結果は、カオス的ダイナミクスが小脳の豊かな時間表現を支える要素となっている可能性を示唆しています。

小脳モデルによって生成された歩行およびボクシングのパターン
図9　Tokuda らによる論文 (Neural Networks, 136, 72–86, 2021) から転載。 © Tokuda et al. 2021. 本図は CC BY 4.0 ライセンスのもとで公開されています。 (a) と (b) は、それぞれ異なる初期入力に対してモデルが生成した歩行およびボクシングのパターンを示しています。 上段のパネルは、モデル出力をスケルトン表示した際のヒトの動きを可視化したもの、 下段のパネルは、骨の角度を表すモデル出力信号の一部を示しています。 図には代表的なトレースのみを抜粋して表示しています。 歩行とボクシングの両方で同じリードアウト結合行列が使用されています。 モデルはヒトのモーションキャプチャデータを学習しており、 可視化には MATLAB Motion Capture Toolbox (https://github.com/lawrennd/mocap) を用いました。

参考文献

  1. Thompson R. F. (2005). In search of memory traces. Annual Review of Psychology, 56, 1–23.
  2. Buonomano, D. V., & Mauk, M. (1994). Neural network model of the cerebellum: Temporal discrimination and the timing of motor responses. Neural Computation, 6(1), 38–55.
  3. Yamazaki, T., & Tanaka, S. (2007). The cerebellum as a liquid state machine. Neural Networks, 20(3), 290–297.
  4. Vervaeke, K., Lorincz, A., Gleeson, P., Farinella, M., Nusser, Z., & Silver, R. A. (2010). Rapid desynchronization of an electrically coupled interneuron network with sparse excitatory synaptic input. Neuron, 67(3), 435–451.
  5. Tsuda, I., Fujii, H., Tadokoro, S., Yasuoka, T., & Yamaguti, Y. (2004). Chaotic itinerancy as a mechanism of irregular changes between synchronization and desynchronization in a neural network. Journal of Integrative Neuroscience, 3(2), 159–182.